Aggregation via the Newtonian potential

This page illustrates the paper Aggregation via the Newtonian potential and aggregation patches (Bertozzi et al., 2012).

Consider the active scalar problem of motion of a function $\rho(x,t)$ by a velocity field \begin{equation} \label{eq:aggregation} v=-\nabla N*\rho \end{equation} where $N$ is the Newtonian potential. Non positive solutions that are compactly supported converge in the long time to a radially symmetric self similar solution.

Equation \eqref{eq:aggregation} has solutions of the form \(\rho(x,t)=h(t)\textbf{1}_{\Omega(t)}(x)\) which we call patch solutions. $\Omega(t)$ is a subset of $\mathbb{R}^N$. Nonnegative patch solutions blow up in finite time. Numerically the patches collapse on skeletons of codimension $1$ (see movies, pictures).

Movies

Below are movies of the time evolution of the boundary of a patch $\Omega(t)$, both in 3D and 2D, for non-negative solutions (attraction) as well as (rescaled) non-positive solutions (repulsion).

For the 2D movies, the red curve is the boundary $\partial\Omega(0)$ of the patch at $t=0$, and the evolving green curve is the boundary $\partial\Omega(t)$ of the patch.

Pictures

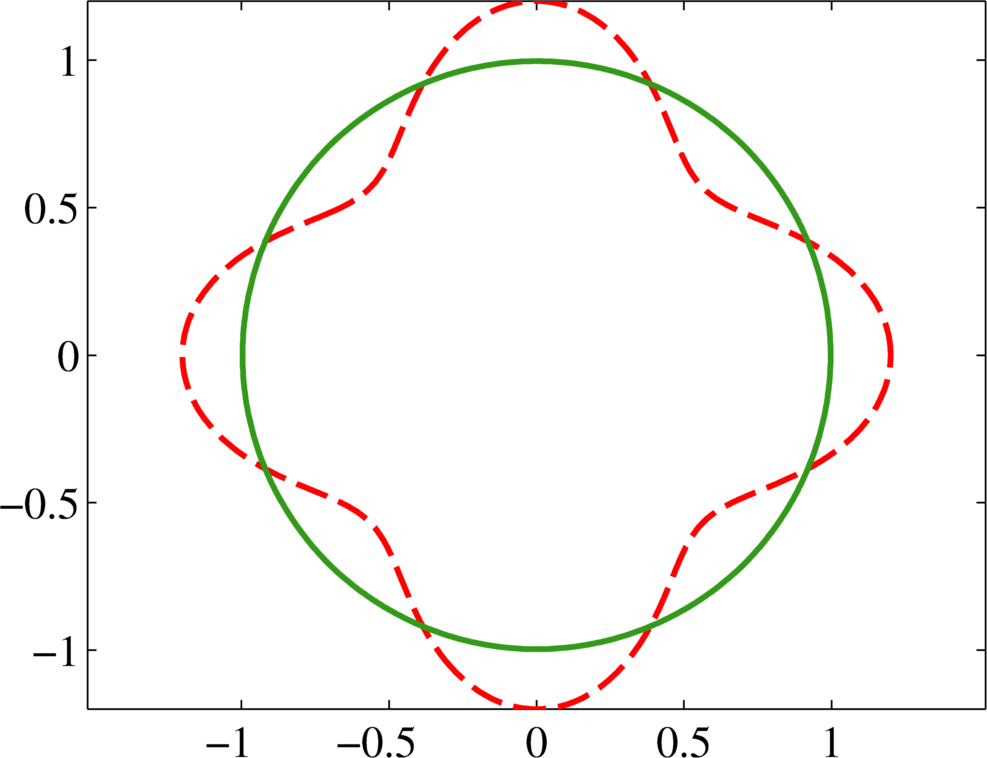
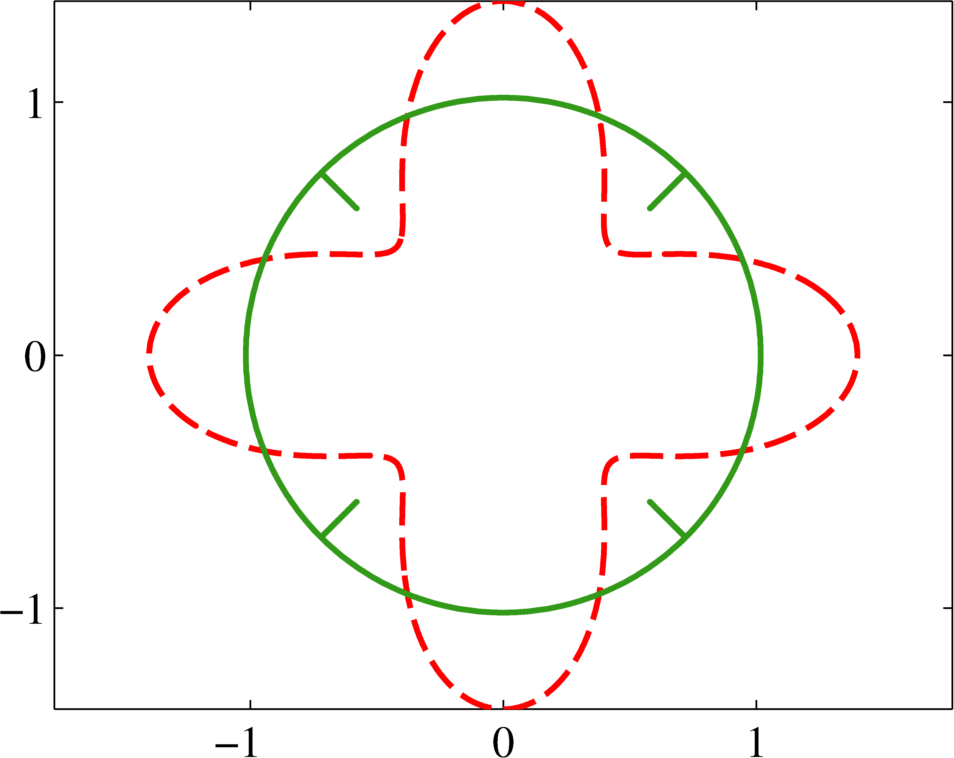
Two examples of contour dynamics for the rescaled spreading problem in two dimensions.

Fig. (a) and (b) show snapshots of the boundary evolution of a patch. At time $s = 10$ the patch has reached steady state. The initial boundary is shown as a red dashed line and the long time limit ($s = 10$) is shown as a green solid line.

Fig. (b) exhibits the “pinching phenomenon” of the boundary.